آموزش تخصصی آمار و معادلات ساختاری

در این مقاله روش معادلات ساختاری با رویکرد بیزی در نرم افزار AMOS آموزش داده می‌شود. یکی از مهم ترین ویژگی‌های نرم افزار AMOS در ویرایش جدید، آن است که با استفاده از روش بیزی می‌تواند به برآورد پارامترها در مدل‌هایی بپردازد که متغیرهای حاضر در آن‌ها از نوع رتبه‌‌‌ای یا اسمی‌هستند. البته این ویژگی در نگارش اولیه این نرم افزار وجود نداشت. به طور کلی مدل سازی معادله ساختاری بیزی از ویژگی‌های ارزشمند نرم افزار AMOS است.

مزایای تحلیل معادلات ساختاری بیزی

1- در مواقعی که حجم نمونه کم است استفاده از رویکرد معادلات ساختاری بیزی مناسب است. در حالی که برآورد حداکثر درست نمایی نسبت به برآورد بیزی در نمونه‌های کوچک، تمایل بیشتری به رد مدل دارد (موتن و آسپاروهو، 2012). هنگامی‌که حجم نمونه زیاد است و همه‌ی پارامترها دارای توزیع نرمال می‌باشند برآورد پارامترهای بیزی و حداکثر درست نمایی یکسان خواهد بود (ون دی شوت و همکاران، 2014).

2- تجزیه و تحلیل بیزی در برخورد با پارامترهایی که توزیع آن‌ها نرمال نیست، می‌تواند دقت بیشتری داشته باشد. به عنوان مثال، برآورد بیزی جایگزین مناسبی برای استفاده از آزمون سوبلو یا انجام بوت استرپ در هنگام آزمون اثرات غیر مستقیم در مدل‌های دارای متغیر میانجی است (ون دی شوت و همکاران، 2014).

3- تجزیه و تحلیل بیزی می‌تواند در حذف پارامترهای غیر قابل قبول مفید باشد. (منفی بودن واریانس و یا بیشتر بودن مقدار همبستگی از یک).

مزایای روش معادلات ساختاری بیزی در نرم افزار AMOS

1- در نرم افزار AMOS، مواقعی که داده پرت وجود داشته باشد امکان این که از روش بوت استرپ برای آزمون اثرات غیر مستقیم استفاده شود وجود ندارد. اگر چه برای این مشکل در ادبیات پیشین راه حل‌هایی پیشنهاد شده است با این حال روش بیزی راه حل راحت تری برای آزمون اثرات غیر مستقیم می‌باشد.

2- روش معمول و استاندارد برآورد پارامتر (برای مثال روش برآورد حداکثر درست نمایی) در نرم افزار AMOS فرض می‌کند متغیرهای تحقیق دارای توزیع نرمال چند متغیره است. زمانی که این فرض نقض می‌شود به ویژه زمانی که متغیر وابسته تحقیق از نوع ترتیبی باشد، روش برآورد بیزین می‌تواند مفید واقع گردد.

توزیع‌های پیشین و پسین

آمار بیزی به طور کلی از یک توزیع خاص پیشین شروع می‌شود. یعنی بیان باور قبلی شخص (قبل از مشاهده داده‌ها) در مورد این که پارامتر مورد نظر به چه صورت در جامعه توزیع شده است (بیرن، 2016). در طول تحلیل بیزین، این باور پیشین با دیتای جدید ترکیب شده و بدین ترتیب توزیع جدیدی بدست می‌آید که به آن توزیع پسین گفته می‌شود (آربوکل، 2017). توزیع پسین بدست آمده در واقع نشان دهنده اطلاعات جدید بروز شده (به وسیله داده) در خصوص پارامتر جمعیت می‌باشد (ون دی شوت و همکاران، 2014).

توزیع پیشین می‌تواند مبتنی بر تحقیقات مهم (از جمله متا آنالیزها) و یا تجربه باشد. در این حالت پیشین محقق، پیشین آگاهی بخش (حاوی اطلاعات مفید) نام دارد. از طرف دیگر اگر اطلاعات پیش زمینه‌‌‌ای کمی‌در خصوص پارامتر جامعه وجود داشته باشد به طوری که آگاهی کمی‌در خصوص پارامتر دهد محقق می‌تواند از پیشین نا آگاهی بخش (دارای اطلاعات غیر مفید) استفاده کند. که در حقیقت یک پیشین نا آگاهی بخش، جهل (نادانی) در خصوص پارامتر جمعیت را نشان می‌دهد.

ارزیابی مدل معادلات ساختاری به روش بیزی

پی-مقدار پسین پیشگویانه (posterior predictive p-value) می‌تواند برای ارزیابی فیت یک مدل واحد استفاده شود. به عبارتی دیگر، این سؤال را مطرح می‌کند که چگونه داده‌های تولید شده (شبیه سازی یا تکرار شده) از روش بیزی با داده‌های مشاهده شده متناسب می‌باشند (کاپلان و دپائولی، 2012).

نحوه قضاوت با پی-مقدار پسین پیشگویانه (posterior predictive p-value)

موتن و آسپاروهو (2012) نشان داده اند که اگر مقدار پی-مقدار پسین پیشگویانه نزدیک به 0.5 باشد مدل تحقیق از برازش بسیار خوبی برخوردار است. با این حال آن‌ها هیچ نوع تئوری و یا اطلاعات تجربی در خصوص این که به چه میزان مقدار (PPP) کم باشد تا محقق مدل را رد کند ارائه نداده اند. آن‌ها پیشنهاد کردند که برای رد یا تایید مدل با مقدار PPP باید بیشتر شبیه به یک شاخص برازش معادلات ساختاری (مانند NFI، GFI و …) برخورد شود تا مانند یک آزمون آماری (Chi-Square). به گفته این نویسندگان، بهتر است آستانه PPP برای رد مدل، در سطوح 1 درصد، 5 درصد و یا 10 درصد در نظر گرفته شود.

همچنین برای ارزیابی مدل شاخص (DIC) وجود دارد که برای مقایسه مدل، با مدل‌های رقیب به روشی شبیه به رویکرد در نظر گرفته شده با معیار AIC استفاده می‌شود. ون دی شوت و همکاران (2017) بیان می‌کند که “با در نظر گرفتن AIC و BIC، مدل‌های با مقدار DIC کمتر باید ترجیح داده شوند.” همچنین ببینید : ( Bayesian Fit Measures).

ارزیابی در خصوص برآورد ضرایب و پارامترها

ارزیابی پارامترهای مدل در رویکرد معادلات ساختاری بیزی توسط فاصله‌های قابل قبول انجام می‌شود. یک فاصله قابل قبول می‌تواند به عنوان “احتمال که پارامتر مورد نظر در یک بازه خاص قرار دارد تعبیر شود” (کاپلان و دپائولی، 2012). این تعریف می‌تواند با معنای فواصل اطمینان در آمار، در تضاد باشد. برای مثال در تعریف فاصله اطمینان داشتیم : 95 درصد فواصل بدست آمده پارامتر مجهول مورد نظر را دربردارند (ون دی شوت و همکاران، 2014).

آزمون فرضیه‌ها در خصوص معنی داری یا عدم معنی داری ضرایب رگرسیونی در روش معادلات ساختاری بیزی در نرم افزار AMOS با استفاده از این فواصل قابل قبول انجام می‌گیرند به طوری که اگر عدد 0 در فاصله قابل قبول ضریب مورد نظر بود، فرض صفر مبنی بر عدم معنی داری ضریب رگرسیونی (ضریب رگرسیونی برابر با صفر است) رد نمی‌گردد.

همگرایی مدل معادلات ساختاری با رویکرد بیزی

معادلات ساختاری بیزی از یک روش مبتنی بر شبیه سازی برای تخمین پارامترهای مدل و توزیع پسین استفاده می‌کند. این امر مستلزم این است که محقق قبل از ارزیابی مناسب بودن مدل، تعیین کند که آیا مدل همگرا شده است یا خیر (بیرن، 2016). یکی از معیارهای همگرایی در نرم افزار AMOS، معیار آماره همگرایی (CS) است. مقدار CS کمتر از 1.002 نشان دهنده همگرایی مدل است. در این مرحله می‌توان شبیه سازی را متوقف کرده و سپس مدل را ارزیابی نمود. (آربوکل، 2017).

نحوه انجام معادلات ساختاری بیزی در نرم افزار AMOS

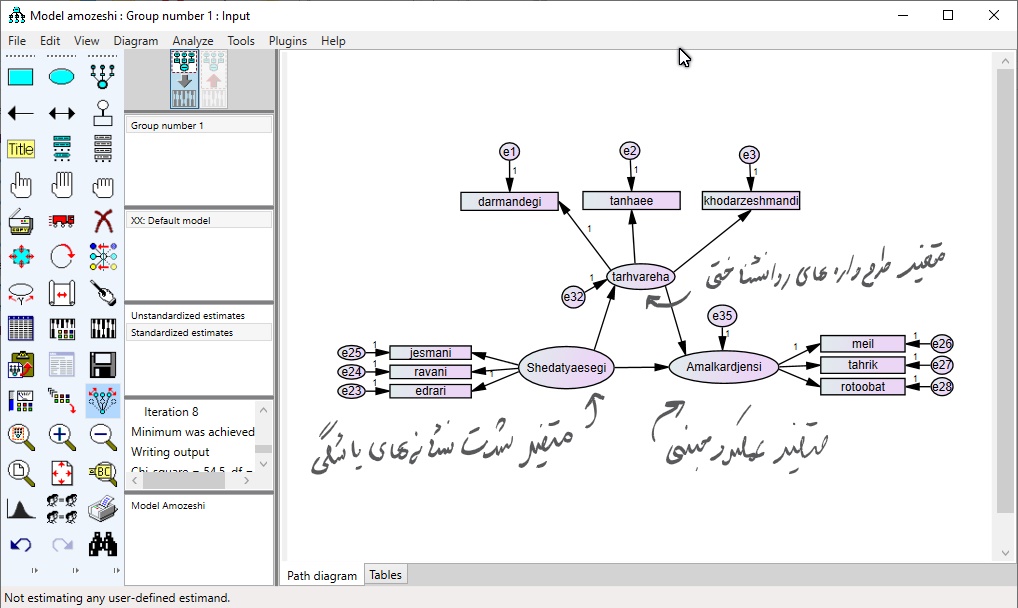
برای تحلیل آماری بیزی در نرم افزار AMOS مدل فرضی زیر را در نظر می‌گیریم. قصد داریم پارامترهای مدل قرار داده شده را به وسیله رویکرد بیزی برآورد کنیم.

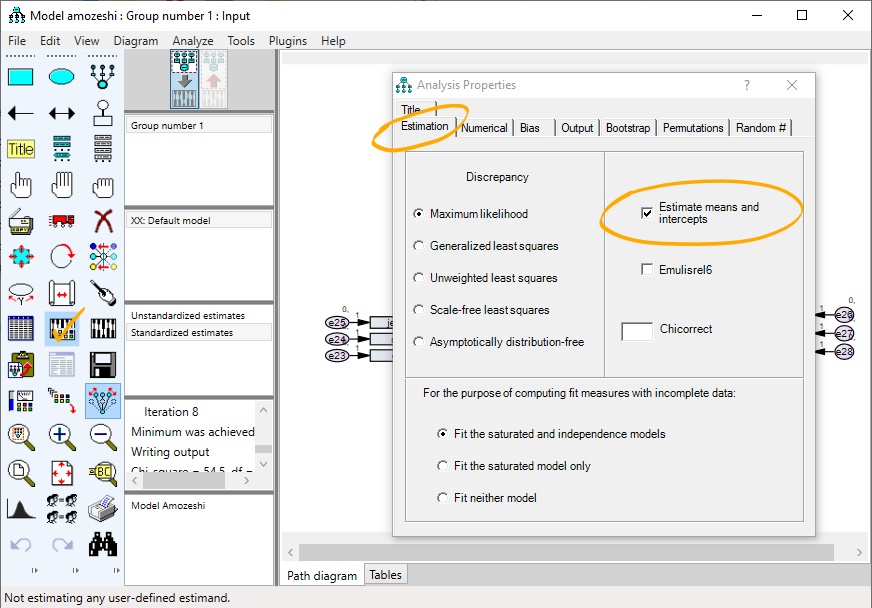
برای برآورد بیزی لازم است تیک گزینه (Estimate means and intercepts) را از زبانه Estimation موجود در پنجره‌ی Analysis Properties مانند شکل زیر فعال شود.

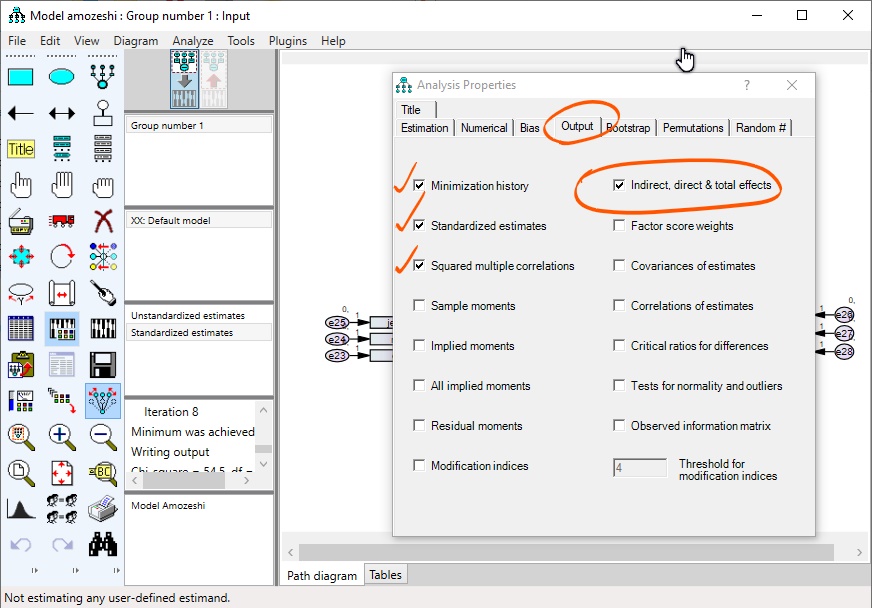
پس از انجام مرحله قبل لازم است که در زبانه Output موجود در پنجره‌ی Analysis Properties تیک گزینه‌های مورد نظر مانند شکل زیر فعال گردد. در اینجا ما قصد داریم مقدار اثرات مستقیم و غیر مستقیم به روش بیزی را مشاهده کنیم.

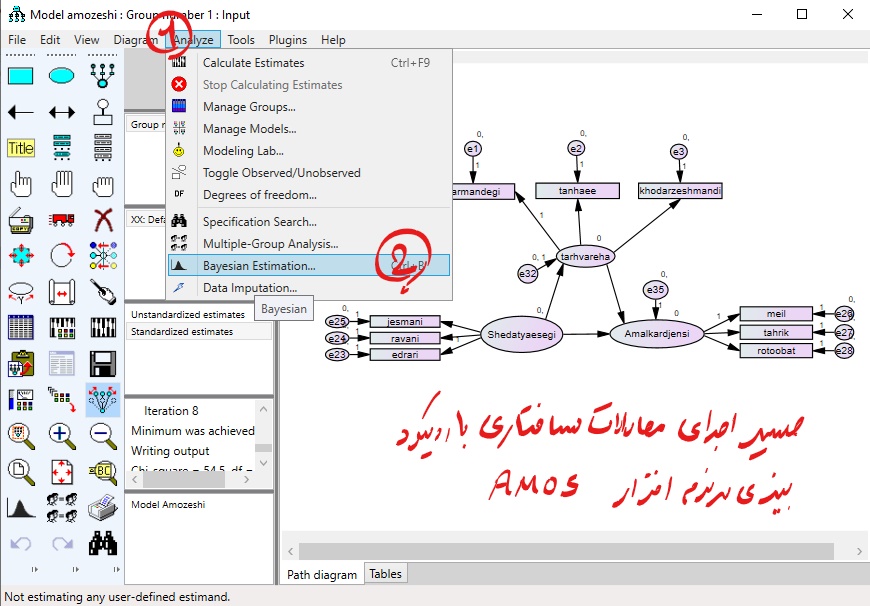
پس از انجام مراحل گفته شده از طریق منوی Analyze مدل را به روش بیزی تخمین می‌زنیم. دستور انجام تحلیل بیزی در نرم افزار AMOS به صورت زیر است :

برآورد پارامترهای مدل به روش بیزی در AMOS

پس از اجرای دستور فوق پنجره جدیدی تحت عنوان Bayesian SEM باز می‌شود. در این زمان، نرم افزار در حال شبیه سازی داده برای برآورد پارامترها است. مقدار پارامترهای بدست آمده مرتبا در حال تغییر هستند و شکلک بالا سمت چپ که بیانگر همگرایی مدل است اگر در حالت ناراحت باشد نشان دهنده عدم همگرایی است و اگر در حالت لبخند باشد نشان دهنده این است که مدل همگرا شده است و می‌توانیم عمل شبیه سازی را متوقت کنیم و به سراغ ارزیابی مدل و پارامترها بپردازیم.

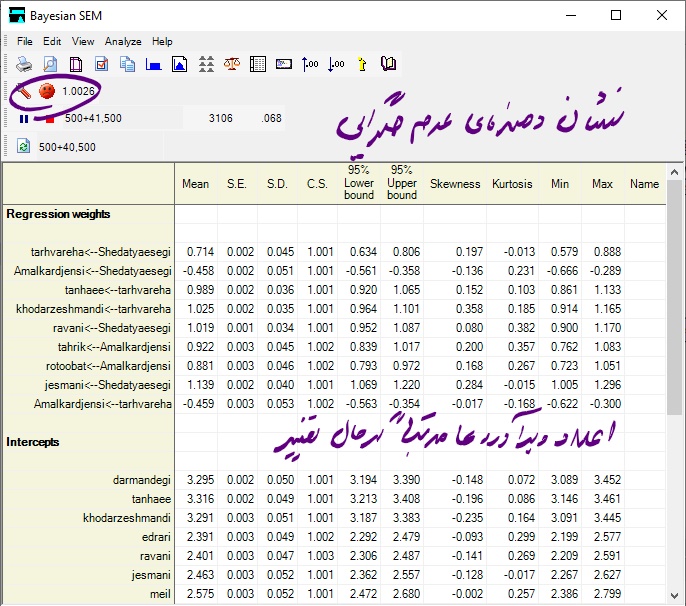
مانند شکل زیر پس از گذشته چند ثانیه مدل به حالت همگرا در می‌آید (شکلک خوشحال) و از آن به بعد برآورد پارامترها با کمترین تغییر عوض می‌شوند. حال وقت آن است که محقق عملیات شبیه سازی را متوقف کند.

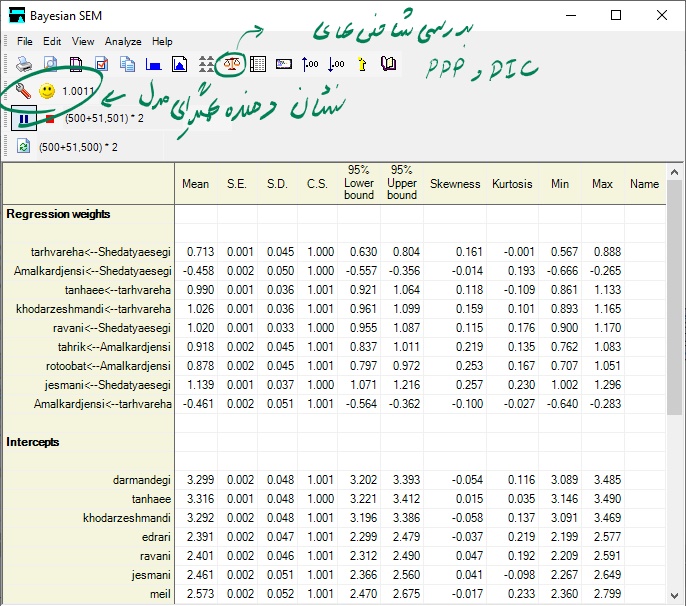
پس از متوقت کردن شبیه سازی، از طریق دکمه مشخص شده در شکل بالا (Fit measures) شاخص‌های ارزیابی برازش مدل را بررسی می‌نماییم.

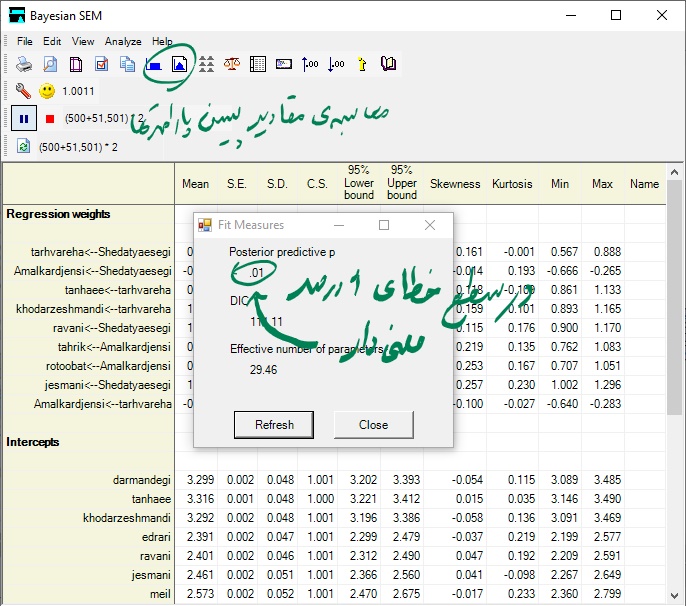
همانطور که مشاهده می‌شود مقدار PPP برابر 0.01 بدست آمده که در سطح خطای 1 درصد قابل قبول است. هر چند همانطوری که در ابتدای مقاله به آن اشاره کردیم نباید به این شاخص به دید آزمون آماری نگاه کرد. بنابراین با مقدار بدست آمده دچار مشکل نخواهیم شد.

توزیع‌های پیشین و پسین در نرم افزار AMOS

پس از کلیک بر روی گزینه (Posterior) در قسمت بعدی مقادیر پسین برای پارامترهای مورد نظر مشاهده می‌شود.

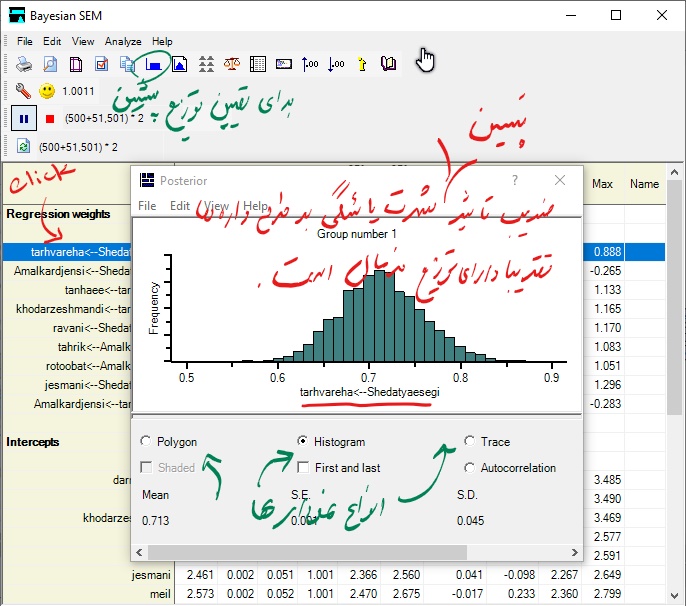
برای بدست آوردن مقدار شاخص‌های پسین مورد نظر (میانگین و انحراف معیار و …) لازم است که پس از باز شدن پنجره Posterior مانند شکل فوق روی پارامتر مورد نظر خود کلیک کنید. همانطوری که از نمودار هیستوگرام ضریب تاثیر شدت نشانه‌های یائسگی بر عملکرد جنسی مشاهده می‌شود، توزیع این پارامتر تقریبا دارای توزیع نرمال است.

همانطوری که در شکل فوق نشان داده شده است با کلیک بر روی دکمه Prior پنجره‌‌‌ای با همین نام مانند شکل زیر باز می‌شود. لازم است که پس از باز شدن پنجره Posterior مانند شکل زیر روی پارامتر مورد نظر خود کلیک کنید.

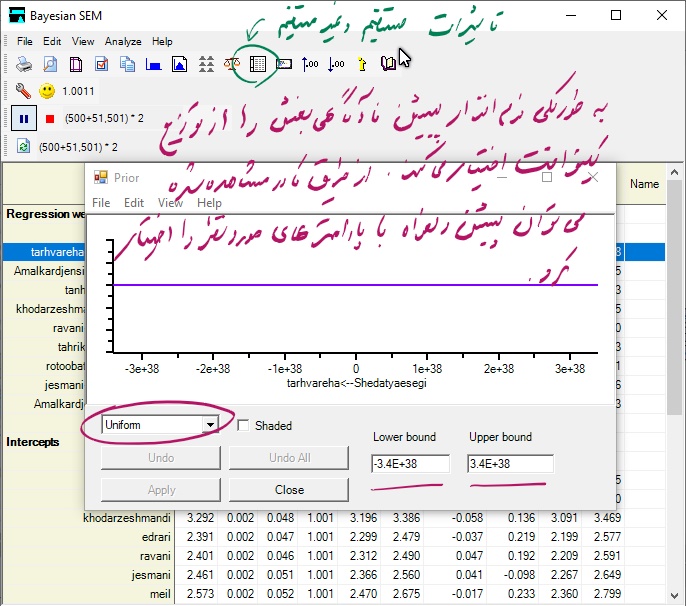
همانطوری که در شکل فوق ملاحظه می‌شود نرم افزار AMOS به صورت پیش فرض از پیشین نا آگاهی بخش یونیفرم (یکنواخت) استفاده می‌کند. از طریق کادر نشان داده شده می‌توان پیشین مورد نظر را انتخاب نمود. همچنین می‌توان توزیع آن را بر روی نمودار رسم کرد.

پس از انجام مراحل فوق وقت آن است که از طریق دکمه (Additional estimands) مقدار اثرات مستقیم و غیر مستقیم متغیرهای تحقیق مشاهده شود. نتایج در شکل زیر گزارش شده است :

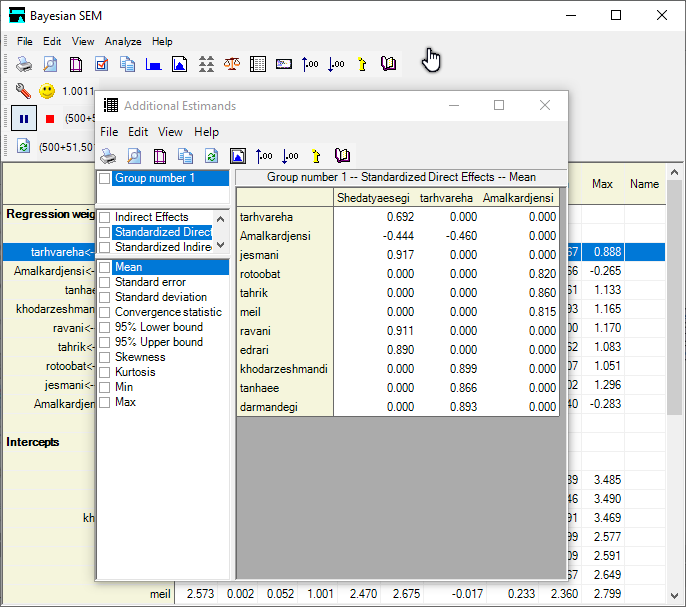
شکل فوق مقادیر اثرات مستقیم استاندارد شده با روش معادلات ساختاری با رویکرد بیزی را نشان می‌دهد. به عنوان مثال اثر مستقیم استاندارد شده تاثیر شدت نشانه‌های یائسگی بر طرحواره‌های روانشناختی برابر 0.692 بدست آمده است.

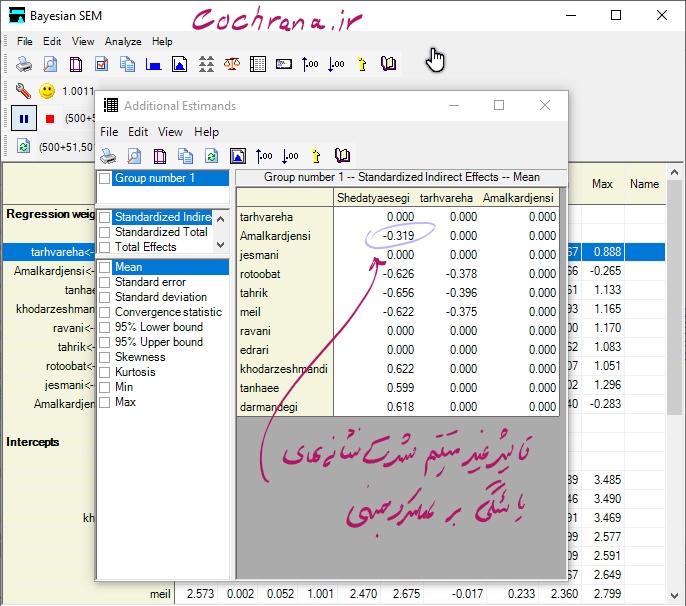
همانطوری که مشاهده می‌شود مقدار اثر غیر مستقیم استاندارد شده شدت نشانه‌های یائسگی بر عملکرد جنسی از طریق متغیر میانجی طرحواره‌های روانشناختی برابر 0.319- بدست آمده است.